Basics

• Project TitleMCAS Summer School Field Day
• ThemeField day activities integrating fitness, biology, Math and ELA
• Submitted ByStephanie Stockwell
• OrganizationWorcester Public Schools
•  

  ---

• Brief DescriptionWorcester Public Schools created an MCAS Summer Camp Field Day on the second to last day of summer school. The field day was held at the athletics fields for Worcester Technical High School. Students from all of the other Worcester summer school locations, Burncoat High School, Doherty High School, Claremont Academy, North High School, South High Community School, Worcester Technical High School, and the Gerald Creamer Center, along with their teachers and site administrators are invited to attend. Students rotate through different stations/workshops with their school. Some stations incorporate ELA, mathematics and/or science into projects that incorporate the track, baseball field, football field, and skateboarding park at the field. This shows students how ELA, mathematics and/or science can be incorporated into exercise and physical education.
• Materials / ResourcesSee list of materials for each activity.
• Team membersDavid Notaro, Stephanie Stockwell
  Activities submitted and led by WPS Summer School Teachers

Units / Activities

• Homeostatis Project (Biology - incorporating ELA and Math)The Module for the Science Lesson began with a large group discussion on what the students knew about their own body and how it reacted to certain parameter changes. We discussed the basic human anatomy and told the students that they would be working today on an inquiry activity to discover how our body maintained its ability to function efficiently even when we changed the parameters. From the group discussion we moved directly into a group activity in which all students participated by running or walking timed intervals around the school‘s circle outside and then simultaneously having their blood pressure, temperature, heart rate, and skin color/perspiration levels recorded. After finishing their rotation members of their group then switched roles so that everyone ran/walked and collected and recorded data. This data was then analyzed in a small group, to discover the changes that our body made in response to the increased exercise and the factors that remained the same. The objective of this module was for the students to understand and see that in order to maintain efficient working standards our bodies maintained what is called homeostasis. The module also addresses all of the learning modalities and keeps the students actively engaged. More importantly, in science education the idea of Inquiry is too often lost and students are simply "told" the answer. Here the students were able to create their own questions and develop, test, and analyze their own ideas and answers.Stopwatch. Blood pressure, thermometer, etc.
• DNA (Biology, Math)This activity addresses the needs of various learners because it is both visual and interactive. instead of simply talking about how DNA makes proteins, the students actively engage in making it themselves. working in teams will help address students who need help or have trouble with this subject. The activity also has a competitive component by making two teams race against one another for students who need a set goal to motivate them.paper plates, yarn and sharpies
• Pitch Game (Math)have students throw a pitch from pitches mound to home plate, time the pitch. the distance is 60 ft, the time is ( ) and solve for the plate. solve for R then convert inches per second to miles per hoursBaseball, baseball glove, stopwatch. See Activity Sheet for calculation details
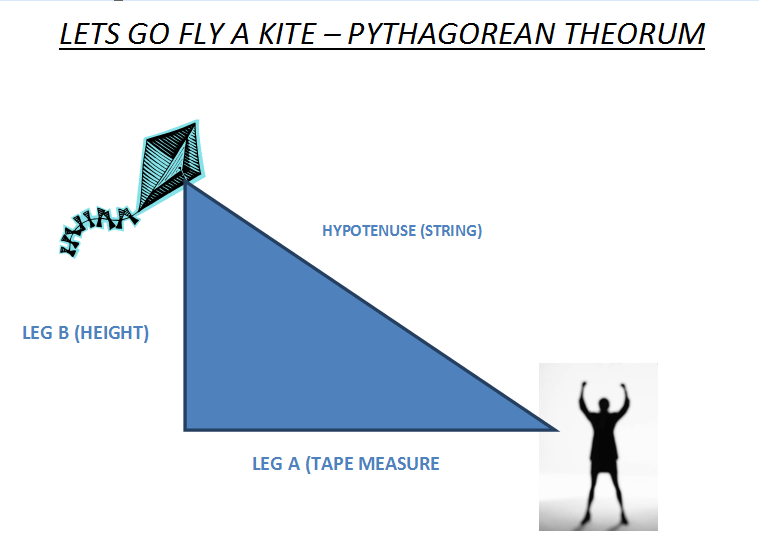
• Kite Height (Math)In conjunction with the Pythagorean theorem lesson, students will fly kites and take measurements to determine how high the kites are above the ground. after a review of the Pythagorean theorem in class student will set up the kites and measure string in 50 foot increments to set a control for the experience. Once the kites are in the air the distance from the flyer to the ground position "under the kite" is measured. the distance and length of the string being used are recorded for calculation of the kite‘s elevation(height about the ground)kites, 100 foot surveyors tapes, kite string and ribbons. See Activity Sheet for details.
•  

  ---

• Finding Slope (Math)Students will break into two even teams. The cones will make up the x and y axis for two graphs. I will then ask students to find the slope of a line with two given points. They can find this by counting the rise over the run on their real life graph or through using the algebraic formula on a white board. I will also ask students to find the y intercept when given the slope and a point that is on the line. I could also ask students to find an equation of a line through another line that is either parallel or perpendicular. The point of this project is to get the students to work together and to have a giant spaced out graph that can provide a large visual to aid their learning process. I will have individual prizes if approved such as candy, and will keep a tally on which team wins for prizes given out at the end of the field day like last year.Cones, white boards
• Imaginary Treasure Land (ELA)as a group, students at this station will take part in a fictional story in which they attempt to overthrow an evil wizard who has been menacing their land.balls, jump rope, cones, hula hoop, prizes, dictionary, thesaurus, paper, pens, markers, pencils, erasers, "spells"
• Aristotle`s Triangle (ELA)Set up a triangle in the field using white rope and stakes, approximately 10 feet per side. Each of the three points of the triangle will be labeled Speaker, Audience, and Subject/Purpose. This can be done with a post and a sign so that the sign is at eye-level. I will also have partial lyrics to 15 well-known songs that incorporate rhetorical devices studied during the summer school class.Rope, posts, signs, lyrics

Activity Sheets

• Kite Height

  Name:_________________________________________Date:________________

  Kite Height

  

  Purpose:  To calculate the height of a kite using Pythagorean Theorem.

  Group Roles: 

  • 1 Writer:  record all data, notes, and sketches during the activity
  • 1 Pilot: flies the kite and is responsible for maintaining the kite’s stability
  • 2 Measurers: use the tape measure to determine all distances
  • 1-2 Aviation Experts (depending on group size): help launch the kite, and ensure that the measurers stand in the correct positions
  • Writer:__________________________
  • Pilot:____________________________
  • Measurers:_______________________; ________________________________
  • Experts:_________________________;________________________________

  Procedure:

  1. Have the measurers determine the length of the string of the kite.If the string is longer than 75 feet, mark off every 50 feet with a piece of ribbon.Record this distance as the hypotenuse of the triangle.

  2. Fly the kite.Once the kite is fully flying with the string fully extended, have the aviation experts and the measurers determine the distance from the pilot to directly underneath the kite (as it’s in the air).Record this distance as the horizontal leg of the triangle.

  3. Sketch the kite flying in the air as a right triangle.Make sure to draw the sketch to scale – use a ruler, and every 10 feet should equal 1 centimeter.For example: If the length of your string is 50 feet, draw a 5 cm hypotenuse.Both the hypotenuse (length of the string) and the horizontal leg (distance from pilot to beneath the kite) should be solid lines.Label both of these sides with the measured distance in feet.Connect the triangle with a dotted vertical line, and label this side as “height”.

  4. Calculate, using the Pythagorean Theorem, the height of the kite.Make sure to list the equation, show all your work, and circle your answer WITH UNITS.

  Sketch:   Draw a sketch of the kite being flown.  Make sure to draw in and label all sides of the triangle with the appropriate measurements.

   

   

   

   

  Calculations:

   

   

   

   

   

  Conclusion:  Answer the following in a paragraph, using complete sentences.

  What was the purpose of the activity?  What were the results?  What obstacles did you encounter during the data collection/measurement?  What suggestions for improvement do you have?  If your kite had a string length (hypotenuse) of 300 feet, and the horizontal length (distance from pilot to beneath the kite) were the same as your measurement, how high would be the kite?  Show your calculation above, include the formula, and your answer with units!!! Explain the results here as well.

• Pitch Game

  Using the equation D=RT                      

  D=distance              
  R=rate                  
  T=time

  Have students throw a pitch from pitches mound to home plate, time the pitch. The distance is 60 ft 6 inches, the time is (  )           
  Solve for R then convert inches per second to miles per hour.

  For example: if my time of pitch was .5 seconds

  D=distance   --->    60ft 6inches  --->   (convert to inches)      ---> 726 inches

  T=time=.5        

  D=RT   

   726/.5 = R (.5)/.5                      

  Solve for R then                    

  R= 1425                       

  1425 inches per second

  Convert to mile per hour.                      

  1425/(12.5280) * 3600 = 82.49 mph

                                      12= inches in ft

                                      5280= ft in mile

                                      3600=seconds in hour

---

Tags = math | fitness | Subject = ELA, Mathematics, Science, Physical_Education_and_Health | Grade Level = HS | Time Period = Summer | Program/Funding = | 632/625 |

---

Direct website link to this project: http://ContextualLearningPortal.org/contextual.asp?projectnumber=390.7519